常微分方程式オイラー編

1階の常微分方程式を近似計算するには差分法という方法があります。
近似する方法として差分近似という考え方を使います。
今回おこなうのは差分近似の中でも前進差分商という方法です。
素直に1度だけの近似計算をするのがオイラー法です。

近似計算する微分方程式は、

\[ \dot y = y \]

で、初期条件は、

\[ y(0) = 1 \]

解は、

\[ y = e^{t} \]

の簡単な微分方程式です。

作成したプログラム

"""
オイラー法を用いて常微分方程式の近似解を求めます。
一次の微分方程式のみ計算できます。
このプログラムでは、0から任意の正の数までの近似点を表示します。
適当な正の数nによって刻み幅が変化します。
"""

import math
import matplotlib.pyplot as plt

def fun(t, y):
    dotY = y
    return dotY

max = 10   # 微分方程式の最大の値(例:最大時間)
n   = 100  # 分割数
y   = 1    # 初期値

# グラフ作成用リスト
tArr   = [0]
yArr   = [y]
idlArr = [y]

dt = max / n # 刻み幅

for i in range(1, n+1):
    t = i * dt
    y += dt * fun(t, y)

    ideal = math.exp(t)
    idlArr.append(ideal)

    tArr.append(t)
    yArr.append(y)

# グラフ作成
plt.plot(tArr, yArr, 'o', label='euler n=100')
plt.plot(tArr, idlArr, label='ideal value')
plt.legend(loc='best')
plt.xlabel('time')
plt.ylabel('y')
plt.show()

できたグラフ

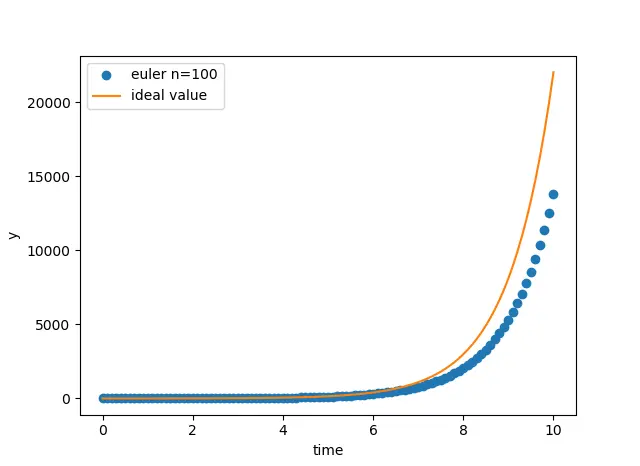
理想的な値はmathライブラリから引っ張ってきました。
分割数がたかだか100だと理想値には程遠いですね。
後の記事にするルンゲ-クッタ法を用いるともっと良くなります。

おまけ

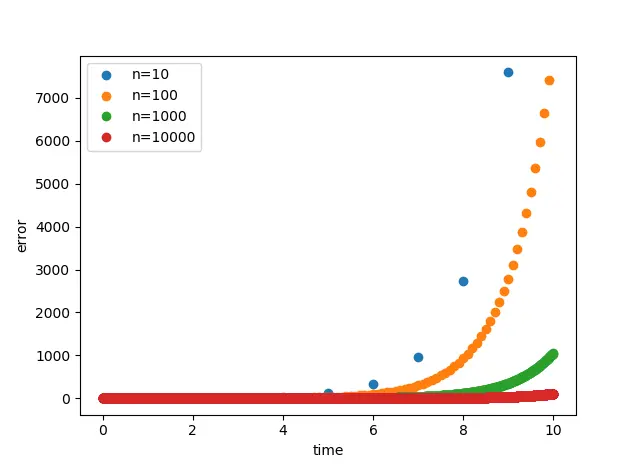
分割数を変えたときのmathライブラリとの差をグラフ化しました。
分割数が10000でもこれなのか（絶望）。
指数関数の悪いところが出ています。
ルンゲ-クッタ法に期待です。