常微分方程式ルンゲ-クッタ編

前回はオイラー法を使って微分方程式の数値計算をしました。
今回はルンゲ-クッタ法という方法を使って数値計算をします。
ルンゲ-クッタ法はざっくり言うと4回近似計算をして、オイラー法よりも精度を上げる工夫がされています。
また、4回の近似計算の中でも重み付けを行っているところも注目したいところです。

近似計算した微分方程式は前回と同じです。

作成したプログラム

"""
ルンゲ-クッタ法を用いて常微分方程式の近似解を求めます。
一次の微分方程式のみ計算できます。
このプログラムでは、0から任意の正の数までの近似点を表示します。
適当な正の数nによって刻み幅が変化します。
"""
import math
import matplotlib.pyplot as plt

def fun(t, y):
    dotY = y
    return dotY

max = 10   # 微分方程式の最大の値(例:最大時間)
n   = 100  # 分割数
y   = 1    # 初期条件

# グラフ作成用リスト
tArr   = [0]
yArr   = [y]
trueArr = [y]

dt = max / n # 刻み幅

for i in range(1, n+1):
    t  = i * dt
    k1 = fun(t, y)
    k2 = fun(t + dt/2, y + dt*k1/2)
    k3 = fun(t + dt/2, y + dt*k2/2)
    k4 = fun(t + dt,   y + dt*k3)
    y += dt/6 * (k1 + 2*k2 + 2*k3 + k4)

    true = math.exp(t)

    tArr.append(t)
    yArr.append(y)
    trueArr.append(true)

plt.plot(tArr, yArr, 'o', label = 'runge-kutta n=100')
plt.plot(tArr, trueArr, label='ideal value')
plt.legend(loc='best')
plt.xlabel('time')
plt.ylabel('y')
plt.show()

できたグラフ

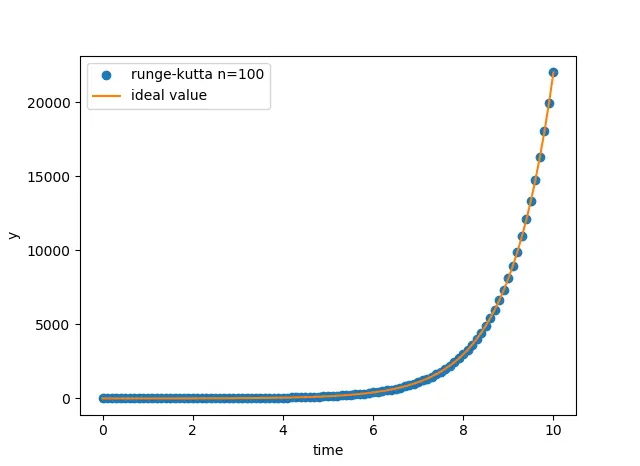
いい感じにできました。
やったね！

おまけ

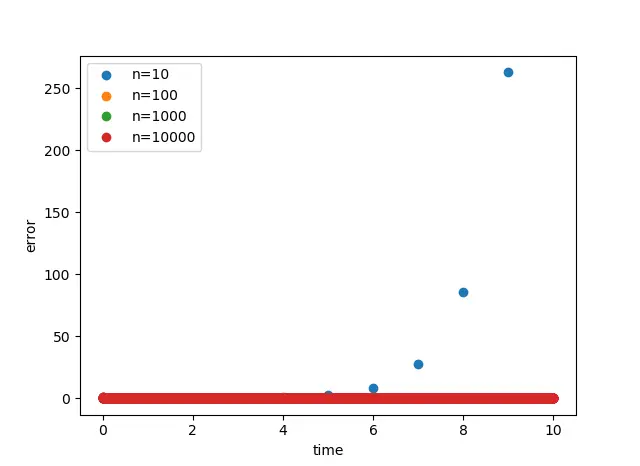
前回と同様に分割数を変えたときのmathライブラリとの比較です。
これじゃあツマラナイので倍率を上げてみると、

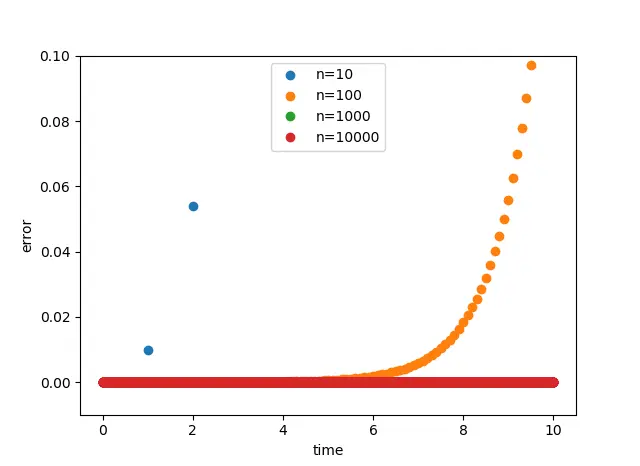
分割数が1000もあれば十分なのがわかります。
4倍の力ってすごいね！