シンプソン則

シンプソン則は台形則のオイシイところを使って、台形則よりも少ない計算数で近似値を求める方法です。

作成したプログラム

"""
シンプソン則を用いて積分値を計算します。
fun関数に計算したい数式を入力して、x0, x1に積分区間を入力すると計算できます。
"""

import math
import matplotlib.pyplot as plt

def fun(x):
    funx = math.cos(x)
    return funx

x0      = 0              # 積分下限数
x1      = 2              # 積分上限数

err     = 1.E-10         # 誤差
partNum = 2              # 分割数
dx      = (x1 - x0) / 2  # 分割幅
trp     = dx * ( fun(x0) + 2*fun( (x0+x1) / 2 ) + fun(x1) ) / 2  # 台形計算
ans     = dx * ( fun(x0) + 4*fun( (x0+x1) / 2 ) + fun(x1) ) / 3  # 答

partNumArr = [partNum]
ansArr     = [ans]

print('partNum      ans')
print(partNum, ans)

for i in range(10):
# 10は適当につけた。多ければ多いほど計算するけど、誤差以下の値になると計算は打ち切られる。
    partNum *= 2
    dx      /= 2
    sum      = 0

    # 新しく分割した台形則の計算
    for j in range(1, partNum, 2) :
        sum += fun(x0 + j*dx)

    new_trp  = trp/2 + dx*sum
    new_ans  = (4*new_trp - trp) / 3

    # 誤差以下だと計算を打ち切る
    if math.fabs(new_ans - ans) < err * math.fabs(new_ans):
        break

    trp  = new_trp
    ans  = new_ans

    partNumArr.append(partNum)
    ansArr.append(new_ans)

    print(partNum, new_ans)

# グラフ描画
plt.plot(partNumArr, ansArr, 'o')
plt.xlabel('number of trials')
plt.ylabel('approximation')
plt.show()

グラフ描画した結果

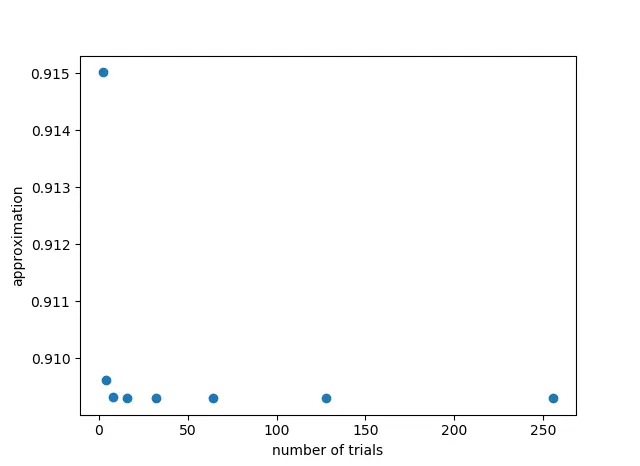
ぱっと見て3～4回計算すれば目標の値になる（適当）。